RELEARN

A Reinforcement Learning header-only template library for C++14. Minimal and simple to use, for a variety of scenarios. It is based on Sutton and Barto’s book and implements some of the functionality described in it.

Currently the library implements Q-Learning for deterministic systems, as well as non-deterministic systems.

The Q-Learning (for both offline and online policy update rule) is:

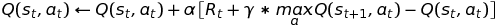
$Q(s_t,a_) = Q(s_t,a_t) + alpha * (R_t + gamma * max(Q_{s+t},a_t) - Q(s_t,a_t))$

The policy decision is entirely up to you to decide; in the case of a deterministic system, usually the options are to either stay on policy:

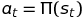
a_t = Π(s_t)

or if using online explorative-greedy (ε-Greedy) assign some decaying probability on using the policy or taking a random action:

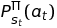
$P_{s_t}^{Π}(a_t)$

For Q-Learning in a non-deterministic system (e.g., when the certainty of transitioning from one state to another is not constant) we use a transition function:

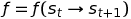
$f = f(s_t,s_{t+1})$

That transition function, suggests that from state s_t if taking action a_t the agent ends up in state s_{t+1}. The assigned probability of that transition must be observed after being taken:

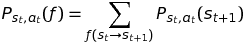
$P(s_t,a_t)(f) = Σ P(s_t,a_t)(s_{t+1})$

This probability quantifies the likelihood of the transition s_t → s_{t+1} for action a_t. Similarly, the Expected reward is:

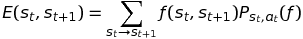
$E(s_t,s_{t+1}) = Σ f(s_t,s_{t+1}) P(s_t,a_t)(f)$

This simply states that the reward is equivalent to the reward of the ending-up state s_{t+1} affected by the transition probability. Therefore, the update rule for probabilistic systems is:

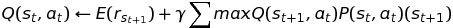
$Q(s_t,a_t) = E(r_{s_{t+1}}) + gamma * Σ maxQ(s_{t+1},a_t)P(s_t,a_t)(s_{t+1})$

Implementation in C++

The template class policy allows the use of your own state and action classes, although a pair of template wrapper classs state and action is provided in the header. You can create your own state and action classes and use them, but they must satisfy the below criteria:

terminal states must have a reward exposed by a method ::reward()
states and actions must be hashable

The classes state and action provided in the header wrap around your own state and action structures, which can be anything, provided they are hashable. Take care to make them unique, otherwise the result may be undefined behaviour.

Markov Decision Process

An MDP is a sequence of States s_t linked together by actions a_t. At the core of relearn is the policy which uses MDPs and maps them using the final state reward R. Whilst multiple episodes may exist, and an episode may be iterated many times, updated, evaluated and re-experienced, the actual process is done in class policy. An overview of an MDP is shown below.

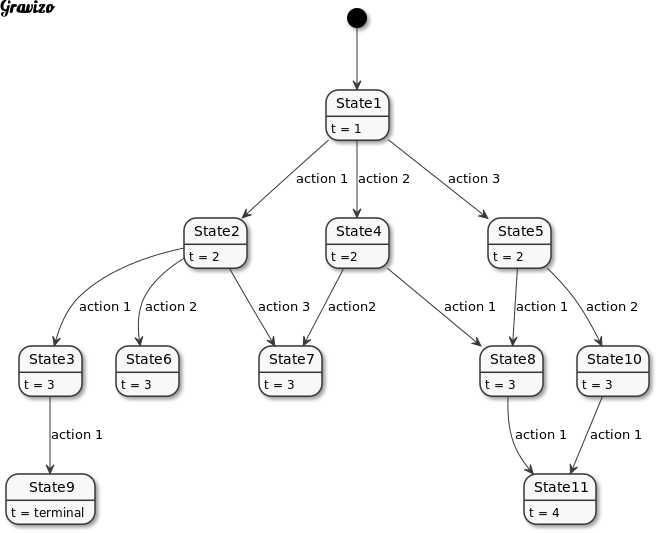
Markov Decision Process

The template parameters state_trait and action_trait are used to describe what a state and action are, the wrappers are used only for indexing, hashing and policy calculation.

The basic use is to create episodes, denoted as markov_chain which you populate as you see fit, and then reward with either a negative (-1), neutral (0) or positive (+1) value.

The use of a markov_chain defaults to an std::deque<relearn::link<state_class,action_class>> where relearn::link is the struct encapsulating a state/action observation.

You may replace the container or link class if you want, but the q_learning structure requires that:

an episode (a markov_chain) can be iterated
there exists an ::size() method to denote the size of the episode

Basically most STL containers should work right out of the box. The library uses by default double for storing and updating Q values, but you can play around with it if needed.

The class that mostly interests us is policy which uses your states and action, and stores them in a map of states, where each state (key) has a value of maps (action to value):

.
├── s_t
|   ├── a_t: 0.03
|   └── a_t: -0.05
├── s_t
|   ├── a_t: -0.001
|   └── a_t: 0.9

You own and control the policy objects, and you can even use multiple ones, however bear in mind that they are not locked for MT access (you have to do this manually). Using q_learning you can then set/update the policy values by iterating your episodes.

Dependencies

There are no external dependencies! However, your compiler must support C++14, so you will need:

gcc 4.8.4 or higher
clang 3.3 or higher

note: I haven’t tested with a Windows platform!

note: If you need serialization, current master branch has a flag USING_BOOST_SERIALIZATION, which when set to ON will enable boost serialization, provided that your states and actions (template parameters state_trait and action_trait are indeed serializable). In this case, you need to use CMake’s find_package to properly find, include and link against boost_serialization.

Building

There is nothing to build! This is a header-only library, you only need to use the relearn.hpp header. However, you may compile the examples in order to see how the library is implemented.

To do that, simply:

mkdir build
cd build
cmake ..
make

build examples

Simply do the following:

cmake .. -DBUILD_EXAMPLES=On
make

build tests

cmake .. -DBUILD_TESTS=On

enable serialization

In order to enable serialization, you need boost and boost-serialization. See your distro on how to install those. To enable it, pass a cmake flag:

cmake .. -DUSING_BOOST_SERIALIZATION=On

For example if you want to run the tests with serialization:

cmake .. -DUSING_BOOST_SERIALIZATION=On -DBUILD_EXAMPLES=On

You can also set this flag for your own project, if you wish to save and load policies, states or actions. Do bear in mind that the state_trait (e.g., your state descriptor) and the action_trait (e.g., your action descriptor) must also be serializable. On how to achieve this, have a look at this tutorial if this condition is not met, you will end up with compilation errors.

Because of the flexibility of boost serialization, you can save and load binary, text or xml archives. Later versions of boost support smart pointers, so even if your descriptors are std::shared_ptr or std::unique_ptr you can still save and load them.

Examples

There is a folder examples which I’m populating with examples, starting from your typical gridworld problem, and then moving on to a blackjack program. Currently there are two “Gridworld” examples:

an offline on-policy algorithm: examples/gridworld_offline.cpp built as ex_gridworld_offline
an online on-policy algorithm: examples/gridworld_online.cpp built as ex_gridworld_online

basic usage

The basic way of using the library is the following:

create a class state, or use an existing class, structure, or PDT which describes (in a Markovian sense) your state
create a class action, or use an existing class, structure, or PDT which describes the action.
create an episode which by default is an std::deque<relearn::link<state,action>> which you populate, and then reward.

At this point, depending on wether you are using an online or offline algorith/approach, you have the following options:

keep creating episodes, obtain a reward for the last/terminal state, and once you have finished, train the policy will all of them, or
every time you create an episode, obtain the reward, then you can train your policy with it.

That choice is up to you, and almost always depends on the domain, system or problem you’re trying to solve. It is for this reason that there is no implementation of on_policy or off_policy or e_greedy, those are very simple algorithms, and are application-specific.

Take a look at the gridworld examples, which demonstrate two different ways of achieving the same task. The blackjack example is different: because playing Blackjack is a probability task, we can’t use a deterministic approach, rather we use a probabilistic approach, in which case

we have to take an offline approach (we don’t know the transition from one state to another until we’ve experienced it)
we have to train on probabilities of transitioning (e.g., non-deterministic)

Gridworld

gridworld image

The pinacle of simplicity when it comes to block/grid world toy problems, our agent resides in a 10x10 gridworld, which is surrounded by blocks into which he can’t move (black colour). The agent starts at blue (x:1,y:8) and the target is the green (x:1,y:1). The red blocks are fire/danger/a negative reward, and there is a rudimentary maze.

There are two versions of the Gridworld, the offline approach:

first the agent randomly explores until it can find the positive reward (+1.0) grid block
then it updates its policies
finally it follows the best policy learnt

And the online approach:

the agent randomly explores one episode
then it updates its policies
then it tries again, this time going after known policies
it only falls back to random when there does not exist a positive best action
the entire process is repeated until the goal is discovered.

The actual gridworld is saved in a textfile gridworld.txt (feel free to change it). The example examples/gridworld_header.hpp provides the minimal code to demonstrate this staged approach. The two files:

examples/gridworld_offline.cpp
examples/gridworld_online.cpp

have the different versions of how this task can be solved.

Once we have loaded the world (using function populate) we set the start at x:1, y:8 and then begin the exploration.

offline q-learning

The offline exploration runs in an inifinite until the grid block with a positive reward is found. Until that happens, the agent takes a stochastic (e.g., random) approach and searches the gridworld. The function (template parameter S is state, and A is action):

template <typename S, 
          typename A>
std::deque<relearn::link<S,A>> explore(const world & w,
                                       std::mt19937 & gen,
                                       grid start);

does the following:

creates a new episode (e.g., relearn::markov_chain)
sets as root state the starting gridblock
randomly picks a direction (see struct rand_direction for more)
repeats this until either (a) a negative reward has been found (e.g., stepped into a fire block), or (b) the goal block is discovered

Each time the expore method is called in the main exploration for loop, an episode is acquired, which is then appended in the list of experienced episodes std::vector<std::deque<relearn::link<state,action>>> episodes.

Once the agent has found the target gridblock, he updates his policy memory using those episodes:

auto learner = relearn::q_learning<state,action>{0.9, 0.1};
for (int k = 0; k < 10; k++) {
    for (auto episode : episodes) {
        learner(episode, policies);
    }
}

In this instance, the agent will run ten iterations for each episode, and the actual Q-Learning parameters are:

alpha (learning rate) 0.9
gamma (discount) 0.1

Finally, once updating policies has finished, the agent proceeds to follow (once) the best action policy:

on_policy(w, policies, start);

The result is that the agent will go straight from x:1, y:8 to x:1, y:1 avoiding any fire blocks and unnecessarily searching the gridworld.

This is a deterministic scenario, because the agent knows at any given moment, which action he is taking, and to which state that action will lead to.

online q-learning

The online exploration is somewhat different, because the explore method does the following:

creates a new episode
sets the root state
if a good policy (Q-value higher than zero and a valid action pointer) exist, it follows them
else if no good policy (or action pointer) exist, it takes a random action
repeats until a reward is found, it then trains the policies with the latest episode

The difference here, is that the actual exploration is instantly affected by what has already be learnt. In comparison, the offline method is not affected, and may repeat the same sequences over and over again. However, if the online version stops too early, there is no guarantee that the agent has learned the ideal or optimal path to the goal, it could in fact be just a mediocre or silly path it has discovered. This of course, is also a problem with offline, where the solution may never be discovered.

Other more complex algorithms exist (e.g., e-greedy) where the agent may follow the policy, but randomly chose to ignore it, in order to try and discover a better solution.

Blackjack

A simplified attempt, where one player uses classic probabilities, the dealer (house) simply draws until 17, and the adaptive agent uses non-deterministic Q-learning in order to play as best as possible.

The state is very simple: a hand which is described by the value (min value and max value, depending on the cards held). The agent ignores the dealer’s hand since that would increase the state space, as well as the label or symbol of the cards held (feel free to change this, simply adapt the “hash” function of hand).

This example takes a lot of time to run, as the agent maps the transitional probabilities, using the observations from playing multiple games.

The header file examples/blackjack_header.hpp contains the simple structures and methods needed to play blackjack, whereas the source file examples/blackjack.cpp has the high level logic behind it.

TODO

do the R-Learning continous algorithm
add eligibility traces (decay)